二叉木、名前の通り、各ノードは最大で 2 つの「叉」、つまり 2 つの子ノードを持ち、左の子ノードと右の子ノードがあります。しかし、二叉木は各ノードが 2 つの子ノードを持つ必要はなく、あるノードは左の子ノードのみ、またあるノードは右の子ノードのみを持つことがあります。
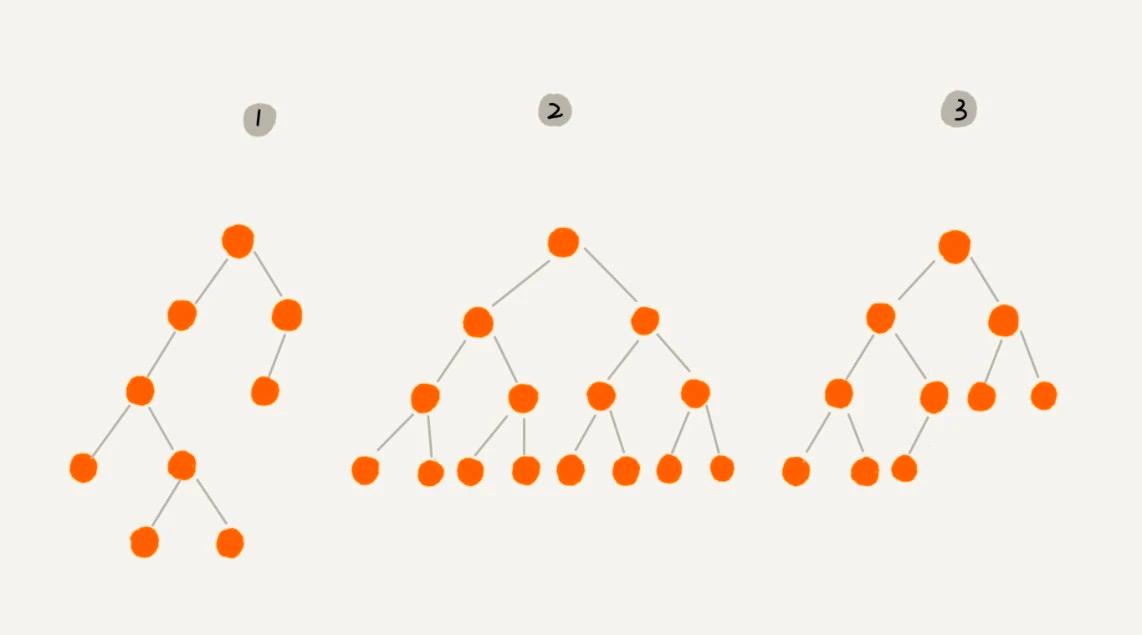
番号 2 の二叉木では、葉ノードはすべて最下層にあり、葉ノードを除いて、各ノードは左右 2 つの子ノードを持っています。このような二叉木を 完全二叉木 と呼びます。
番号 3 の二叉木では、葉ノードは最下の 2 層にあり、最後の層の葉ノードは左に並んでおり、最後の層を除く他の層のノード数は最大に達する必要があります。このような二叉木を 完全二叉木 と呼びます。
二叉木をどのように表現(または保存)するか?#
1 つはポインタまたは参照に基づく二叉 連結ストレージ法、もう 1 つは配列に基づく 順序ストレージ法 です。
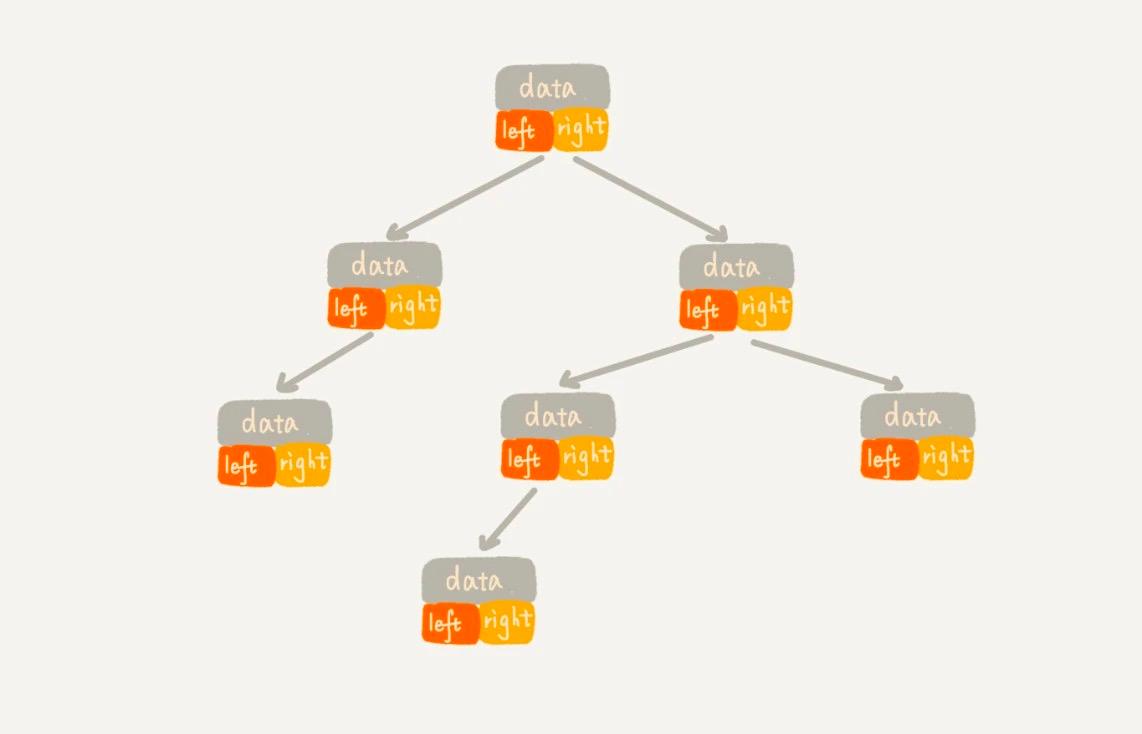
連結ストレージ法。図からわかるように、各ノードには 3 つのフィールドがあり、そのうちの 1 つはデータを保存し、他の 2 つは左右の子ノードを指すポインタです。根ノードを持っていれば、左右の子ノードのポインタを通じて、全体の木をつなげることができます。このストレージ方式は一般的に使用されます。ほとんどの二叉木のコードはこの構造を使用して実装されています。
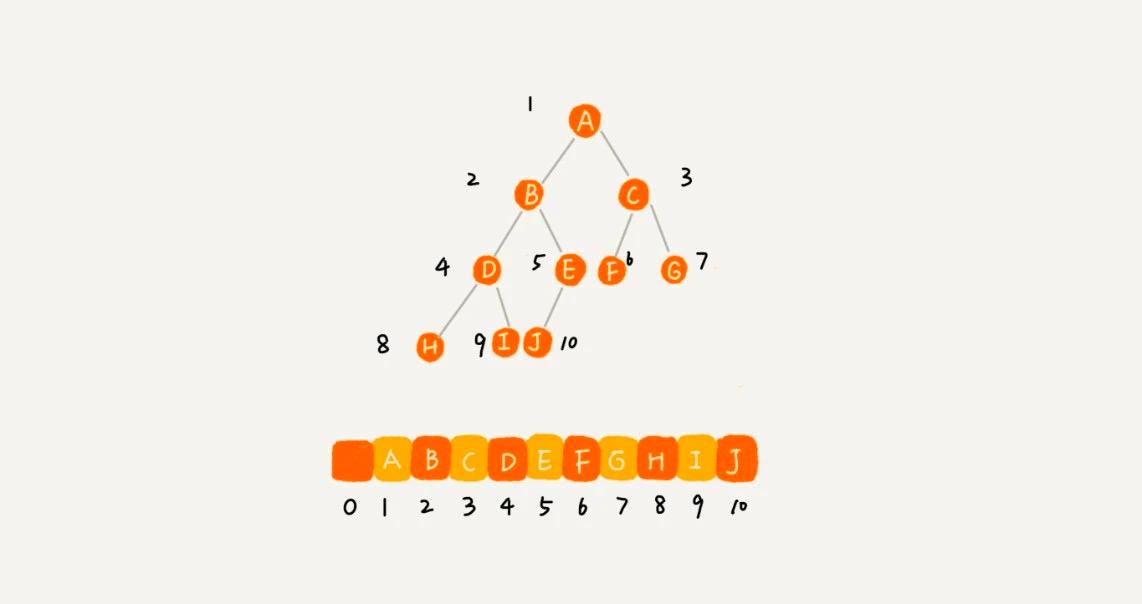
配列に基づく順序ストレージ法。根ノードをインデックス i = 1 の位置に保存し、左の子ノードはインデックス 2 * i = 2 の位置に、右の子ノードは 2 * i + 1 = 3 の位置に保存します。これを繰り返すと、B ノードの左の子ノードは 2 * i = 2 * 2 = 4 の位置に、右の子ノードは 2 * i + 1 = 2 * 2 + 1 = 5 の位置に保存されます。
先ほどの例は完全二叉木であるため、インデックス 0 のストレージ位置を「無駄に」しているだけです。非完全二叉木の場合、実際にはかなり多くの配列ストレージスペースが無駄になります。以下の例を見てみましょう。
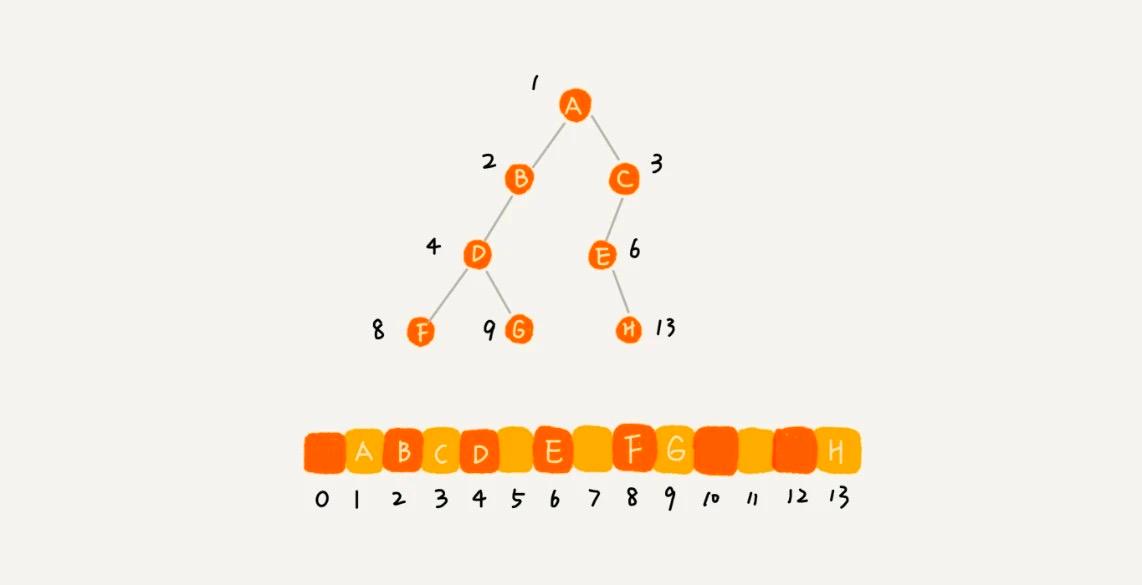
したがって、ある二叉木が完全二叉木である場合、配列での保存は間違いなく最もメモリを節約する方法です。配列のストレージ方式は、連結ストレージ法のように左右の子ノードのポインタを追加で保存する必要がないからです。これが完全二叉木が特別に取り上げられる理由であり、完全二叉木が最後の層の子ノードを左に揃える必要がある理由でもあります。
二叉木の遍歴#
古典的な方法は 3 つあり、前順遍歴、中順遍歴、後順遍歴です:
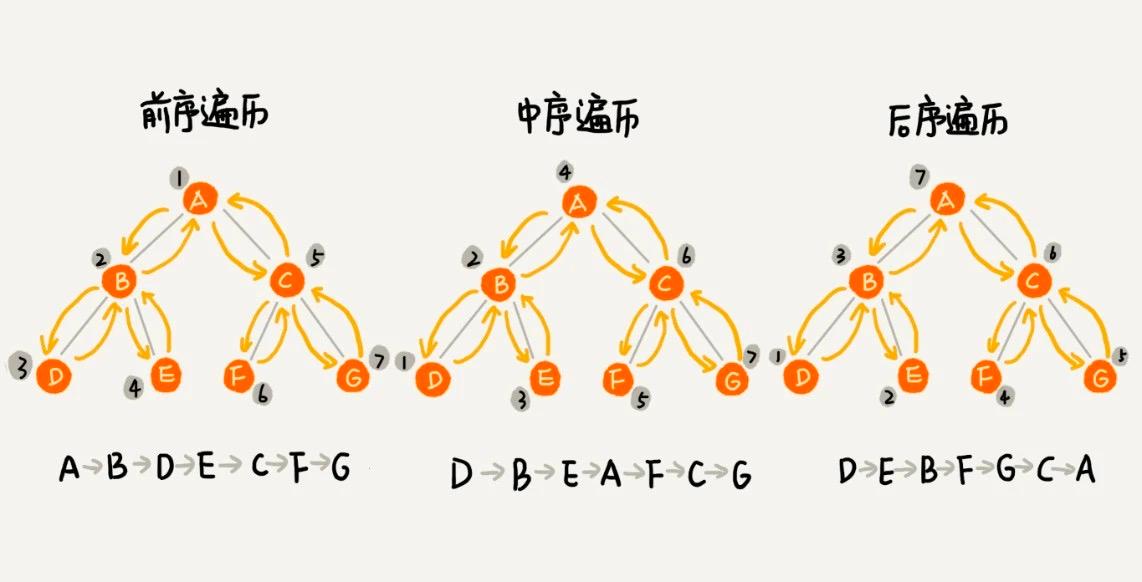
- 前順遍歴:木の任意のノードに対して、まずこのノードを印刷し、次にその左の子木を印刷し、最後にその右の子木を印刷します。
- 中順遍歴:木の任意のノードに対して、まずその左の子木を印刷し、次にそのノード自体を印刷し、最後にその右の子木を印刷します。
- 後順遍歴:木の任意のノードに対して、まずその左の子木を印刷し、次にその右の子木を印刷し、最後にこのノード自体を印刷します。
実際には、遍歴自体のノードの順序の問題です。
// 先序
function preOrder(root) {
if (root == null) return;
console.log(root.value);
preOrder(root.left);
preOrder(root.right);
}
// 中序
function inOrder(root) {
if (root == null) return;
inOrder(root.left);
console.log(root.value);
inOrder(root.right);
}
// 後序
function postOrder(root) {
if (root == null) return;
postOrder(root.left);
postOrder(root.right);
console.log(root.value);
}
二叉探索木#
二叉検索木とも呼ばれ、二叉探索木の最大の特徴は、動的データ集合の迅速な挿入、削除、検索操作をサポートすることです。
二叉探索木は、木の任意のノードにおいて、その左の子木の各ノードの値がこのノードの値より小さく、右の子木のノードの値がこのノードの値より大きいことを要求します。

1. 二叉探索木の検索操作#
まず根ノードを取り、その値が検索したいデータと等しい場合は返します。検索したいデータが根ノードの値より小さい場合は左の子木で再帰的に検索し、検索したいデータが根ノードの値より大きい場合は右の子木で再帰的に検索します。

function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
function searchBST(root, val) {
while (root !== null && val !== root.val) {
root = val < root.val ? root.left : root.right;
}
return root;
}
2. 二叉探索木の挿入操作#
挿入したいデータがノードのデータより大きく、ノードの右の子木が空であれば、新しいデータを右の子ノードの位置に直接挿入します。空でない場合は、右の子木を再帰的に遍歴して挿入位置を探します。同様に、挿入したいデータがノードの値より小さく、ノードの左の子木が空であれば、新しいデータを左の子ノードの位置に挿入します。空でない場合は、左の子木を再帰的に遍歴して挿入位置を探します。

function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
function insertBST(root, val) {
if (root === null) {
root = new TreeNode(val);
return root;
}
while (root != null) {
if (val > root.val) {
if (root.right == null) {
root.right = new TreeNode(val);
return root;
}
root = root.right;
} else {
if (root.left == null) {
root.left = new TreeNode(val);
return root;
}
root = root.left;
}
}
}
3. 二叉探索木の削除操作#
削除するノードの子ノードの数に応じて、3 つのケースに分けて処理する必要があります。
- 削除するノードに子ノードがない場合、親ノードの削除するノードを指すポインタを null に設定するだけです。例えば、図の削除ノード 55。
- 削除するノードに子ノードが 1 つ(左の子ノードまたは右の子ノードのみ)の場合、親ノードの削除するノードを指すポインタを削除するノードの子ノードを指すように更新するだけです。例えば、図の削除ノード 13。
- 削除するノードに子ノードが 2 つある場合、これは比較的複雑です。このノードの右の子木の最小ノードを見つけ、それを削除するノードに置き換えます。その後、この最小ノードを削除します。最小ノードには左の子ノードがないため(もしあれば、それは最小ノードではありません)、上記の 2 つのルールを適用してこの最小ノードを削除できます。例えば、図の削除ノード 18。

function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
function deleteNode(root, key) {
if (!root) return null;
if (root.val > key) {
root.left = deleteNode(root.left, key);
return root;
}
if (root.val < key) {
root.right = deleteNode(root.right, key);
return root;
}
if (root.val === key) {
if (!root.left && !root.right) {
return null;
}
if (!root.right) {
return root.left;
}
if (!root.left) {
return root.right;
}
let p = root.right;
while (p.left) {
p = p.left;
}
root.right = deleteNode(root.right, p.val);
p.right = root.right;
p.left = root.left;
return p;
}
};
平衡二叉探索木#
平衡二叉木:二叉木の任意のノードの左右の子木の高さの差は 1 を超えてはなりません。この定義から見ると、完全二叉木や満二叉木は実際には平衡二叉木ですが、非完全二叉木も平衡二叉木である可能性があります。

平衡二叉探索木は、上記の平衡二叉木の定義を満たすだけでなく、二叉探索木の特徴も満たします。最初に発明された平衡二叉探索木はAVL木であり、これは平衡二叉探索木の定義に厳密に従い、任意のノードの左右の子木の高さの差が 1 を超えない、高さがバランスの取れた二叉探索木です。
平衡二叉探索木のようなデータ構造を発明した目的は、通常の二叉探索木が頻繁な挿入、削除などの動的更新の状況で、時間計算量が劣化する問題を解決することです。
したがって、平衡二叉探索木における「平衡」とは、木全体が左右で比較的「対称的」または「バランスの取れた」状態を保ち、左の子木が非常に高く、右の子木が非常に低い状態を避けることを意味します。これにより、木全体の高さが相対的に低くなり、挿入、削除、検索などの操作の効率が向上します。
赤黒木#
赤黒木の英語は「Red-Black Tree」で、略して R-B Tree と呼ばれます。これは厳密ではない平衡二叉探索木です。赤黒木のノードは、1 つのクラスが黒色に、もう 1 つのクラスが赤色にマークされています。さらに、赤黒木は以下のいくつかの要件を満たす必要があります:
- 根ノードは黒色である
- 各葉ノードは黒色の空ノードであり、つまり葉ノードはデータを保存しない
- 隣接するノードは同時に赤色であってはならない、つまり赤色ノードは黒色ノードによって隔てられている
- 各ノードから、そのノードに到達可能な葉ノードまでのすべてのパスには、同じ数の黒色ノードが含まれている